To hinge or not to hinge? That is the question: How we use hinge questions in maths
When students aren’t sitting in front of you, how do we check they understand the work? How do we know when to adapt our teaching?

One of the main worries for any teacher is ‘What do I do if the students don’t understand what I’m teaching them?’, but really the biggest question is ‘HOW do I know if the students understand what I’m teaching them?’
In face-to-face teaching, students have a multitude of ways of letting the teacher know that something isn’t quite adding up. A raised hand, a confused look, and distraction techniques that are linked to poor behaviour. Some are obvious, while others are subtle. But any teacher will tell you one thing that happens if their class don’t understand a topic; they know about it straight away.
At Academy21, we need different ways of judging our students’ understanding. In maths, we use multiple-choice hinge questions to gauge, understand, and decide which direction to take the lesson. Have the students grasped the key concepts? Or are they in need of further examples? This allows us to be dynamic and adaptive in our live teaching.
What does the research say about the benefits of hinge questions?
- Cognitive Load Theory: This theory suggests that well-designed multiple-choice questions can reduce cognitive load by focusing students on specific key concepts, allowing them to process and apply information more effectively.
- Formative Assessment Principles: Studies have shown that formative assessments can significantly improve student learning by offering timely feedback and opportunities for self-reflection. Hinge questions provide a proactive approach to formative assessment.
- Diagnostic Teaching: Multiple-choice questions can reveal common misconceptions or errors in students’ thinking. By analysing patterns in student responses, teachers can identify and address misunderstandings quickly.
- Engagement and Motivation: Research indicates that students are more engaged when they are actively involved in the learning process. Multiple-choice hinge questions can stimulate critical thinking and maintain student interest.
- Data-Driven Instruction: The immediate feedback from hinge questions allows teachers to make data-driven decisions about curriculum pacing and modification, tailoring instruction to meet the specific needs of their students.
What does a good hinge question look like?
- Diagnostic: It should be able to diagnose misconceptions or gaps in understanding. The distractors (incorrect options) should be based on common errors or misunderstandings, providing insights into students’ thinking.
- Focused: The question should target a specific concept or skill that is crucial for the lesson’s learning objectives. It should address the “hinge point” in the lesson where understanding is essential for moving forward.
- Concise and Clear: The question and options should be clearly worded and concise, avoiding unnecessary complexity that could confuse students
- Time-efficient: Students should be able to answer the question in a short amount of time, typically in under two minutes, to facilitate quick assessment during a lesson.
- Stimulating Thought: The question should require students to apply their knowledge rather than recall facts. It should encourage critical thinking and reasoning.
- Unambiguous: There should be a clearly correct answer among the options provided. The question and its context should leave no room for interpretation that could lead to multiple valid answers.
- Relevant and Contextual: The question should be relevant to the lesson and presented in a context that makes sense to students, helping them to relate the question to real-world scenarios or previously learned concepts.
- Inclusive: The language and context should be accessible to all students, avoiding cultural biases or assumptions that might disadvantage some learners.
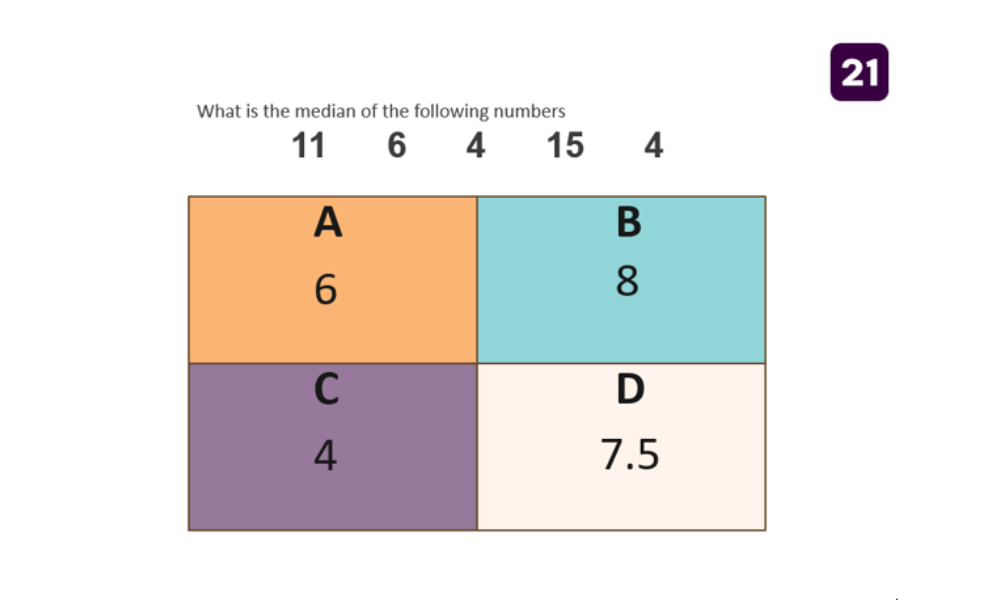
Here is an example of a hinge question used to assess a student’s understanding of finding the median. If relevant examples have been used, this question is accessible to all. It is clear what the students are expected to do. The incorrect answers relate to the mode, mean and midpoint of the highest and lowest values, all common misconceptions when finding the median. This question allows the teacher to not only check whether students know how to find the median, but also identify any misconceptions and address them immediately.
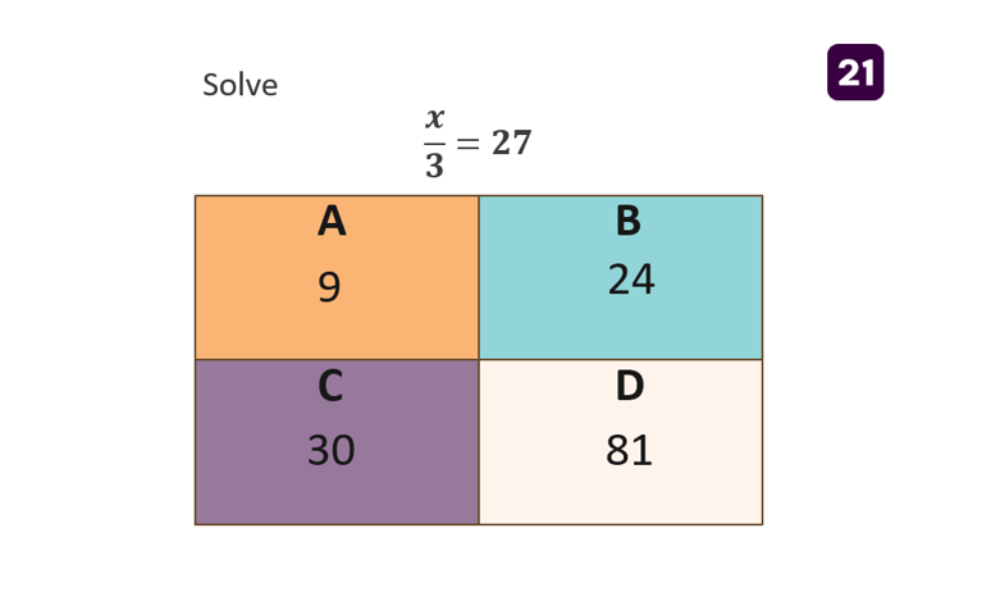
This question is once again very clear and concise. It can be done quickly and requires an understanding of solving 1-step equations. The three incorrect options are again common misconceptions surrounding which inverse operation to use to solve the equation.
A series of these questions can be used throughout the lesson to check understanding and adapt the lesson. The numbers in the equation question above can be easily altered to allow a second attempt if students were confused at first. The use of polls in the online classroom is a fantastic way to ensure that answers can be seen by the teacher quickly and confidentially.
At Academy 21, our live, online delivery means we have the capability to be responsive and fast with our formative assessment. For maths in particular, well-planned hinge questions can allow an insight into the students’ minds without even needing to see them.



